Generating counterbalanced orders
Problem
You want to generate counterbalanced sequences for an experiment.
Solution
The function latinsquare() (defined below) can be used to generate Latin squares.
latinsquare(4)
#> [,1] [,2] [,3] [,4]
#> [1,] 1 2 4 3
#> [2,] 2 1 3 4
#> [3,] 3 4 1 2
#> [4,] 4 3 2 1
# To generate 2 Latin squares of size 4 (in sequence)
latinsquare(4, reps=2)
#> [,1] [,2] [,3] [,4]
#> [1,] 3 4 1 2
#> [2,] 4 3 2 1
#> [3,] 1 2 4 3
#> [4,] 2 1 3 4
#> [5,] 4 2 1 3
#> [6,] 2 3 4 1
#> [7,] 1 4 3 2
#> [8,] 3 1 2 4
# It is better to put the random seed in the function call, to make it repeatable
# This will return the same sequence of two Latin squares every time
latinsquare(4, reps=2, seed=5873)
#> [,1] [,2] [,3] [,4]
#> [1,] 1 4 2 3
#> [2,] 4 1 3 2
#> [3,] 2 3 4 1
#> [4,] 3 2 1 4
#> [5,] 3 2 4 1
#> [6,] 1 4 2 3
#> [7,] 4 3 1 2
#> [8,] 2 1 3 4
There are 576 Latin squares of size 4. The latinsquare function will, in effect, randomly select n of these squares and return them in sequence. This is known as a replicated Latin square design.
Once you generate your Latin squares, it is a good idea to inspect them to make sure that there are not many duplicated sequences. This is not uncommon with smaller squares (3x3 or 4x4).
A function for generating Latin squares
This function generates Latin squares. It uses a somewhat brute-force algorithm to generate each square, which can sometimes fail because it runs out of available numbers to put in a given location. In such cases, it just tries again. There may be an elegant way out there to do it, but I am not aware of it.
## - len is the size of the latin square
## - reps is the number of repetitions - how many Latin squares to generate
## - seed is a random seed that can be used to generate repeatable sequences
## - returnstrings tells it to return a vector of char strings for each square,
## instead of a big matrix. This option is only really used for checking the
## randomness of the squares.
latinsquare <- function(len, reps=1, seed=NA, returnstrings=FALSE) {
# Save the old random seed and use the new one, if present
if (!is.na(seed)) {
if (exists(".Random.seed")) { saved.seed <- .Random.seed }
else { saved.seed <- NA }
set.seed(seed)
}
# This matrix will contain all the individual squares
allsq <- matrix(nrow=reps*len, ncol=len)
# Store a string id of each square if requested
if (returnstrings) { squareid <- vector(mode = "character", length = reps) }
# Get a random element from a vector (the built-in sample function annoyingly
# has different behavior if there's only one element in x)
sample1 <- function(x) {
if (length(x)==1) { return(x) }
else { return(sample(x,1)) }
}
# Generate each of n individual squares
for (n in 1:reps) {
# Generate an empty square
sq <- matrix(nrow=len, ncol=len)
# If we fill the square sequentially from top left, some latin squares
# are more probable than others. So we have to do it random order,
# all over the square.
# The rough procedure is:
# - randomly select a cell that is currently NA (call it the target cell)
# - find all the NA cells sharing the same row or column as the target
# - fill the target cell
# - fill the other cells sharing the row/col
# - If it ever is impossible to fill a cell because all the numbers
# are already used, then quit and start over with a new square.
# In short, it picks a random empty cell, fills it, then fills in the
# other empty cells in the "cross" in random order. If we went totally randomly
# (without the cross), the failure rate is much higher.
while (any(is.na(sq))) {
# Pick a random cell which is currently NA
k <- sample1(which(is.na(sq)))
i <- (k-1) %% len +1 # Get the row num
j <- floor((k-1) / len) +1 # Get the col num
# Find the other NA cells in the "cross" centered at i,j
sqrow <- sq[i,]
sqcol <- sq[,j]
# A matrix of coordinates of all the NA cells in the cross
openCell <-rbind( cbind(which(is.na(sqcol)), j),
cbind(i, which(is.na(sqrow))))
# Randomize fill order
openCell <- openCell[sample(nrow(openCell)),]
# Put center cell at top of list, so that it gets filled first
openCell <- rbind(c(i,j), openCell)
# There will now be three entries for the center cell, so remove duplicated entries
# Need to make sure it's a matrix -- otherwise, if there's just
# one row, it turns into a vector, which causes problems
openCell <- matrix(openCell[!duplicated(openCell),], ncol=2)
# Fill in the center of the cross, then the other open spaces in the cross
for (c in 1:nrow(openCell)) {
# The current cell to fill
ci <- openCell[c,1]
cj <- openCell[c,2]
# Get the numbers that are unused in the "cross" centered on i,j
freeNum <- which(!(1:len %in% c(sq[ci,], sq[,cj])))
# Fill in this location on the square
if (length(freeNum)>0) { sq[ci,cj] <- sample1(freeNum) }
else {
# Failed attempt - no available numbers
# Re-generate empty square
sq <- matrix(nrow=len, ncol=len)
# Break out of loop
break;
}
}
}
# Store the individual square into the matrix containing all squares
allsqrows <- ((n-1)*len) + 1:len
allsq[allsqrows,] <- sq
# Store a string representation of the square if requested. Each unique
# square has a unique string.
if (returnstrings) { squareid[n] <- paste(sq, collapse="") }
}
# Restore the old random seed, if present
if (!is.na(seed) && !is.na(saved.seed)) { .Random.seed <- saved.seed }
if (returnstrings) { return(squareid) }
else { return(allsq) }
}
Testing the function for randomness
Some algorithms for generating Latin squares may not create them very randomly. There are 576 unique 4x4 squares, and each one should have an equal probability of being created, but some algorithms do not properly do this. There is probably no need to test the randomness of the function above, but here is some code that will do it. Previous algorithms that I used did not have a good random distribution, which was discovered by running the code below.
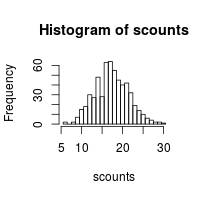
This code creates 10,000 4x4 Latin squares, then counts how often each of the 576 unique squares appears. The counts should form a not-too-wide normal distribution; otherwise the distribution not very random. I believe the expected standard deviation of the distribution (assuming randomly generated squares) is sqrt(10000/576).
# Set up the size and number of squares to generate
squaresize <- 4
numsquares <- 10000
# Get number of unique squares of a given size.
# There is not a general solution to finding the number of unique nxn squares
# so we just hard-code the values here. (From http://oeis.org/A002860)
uniquesquares <- c(1, 2, 12, 576, 161280, 812851200)[squaresize]
# Generate the squares
s <- latinsquare(squaresize, numsquares, seed=122, returnstrings=TRUE)
# Get the list of all squares and counts for each
slist <- rle(sort(s))
scounts <- slist[[1]]
hist(scounts, breaks=(min(scounts):(max(scounts)+1)-.5))
cat(sprintf("Expected and actual standard deviation: %.4f, %.4f\n",
sqrt(numsquares/uniquesquares), sd(scounts) ))
#> Expected and actual standard deviation: 4.1667, 4.0883